MESH GENERATION
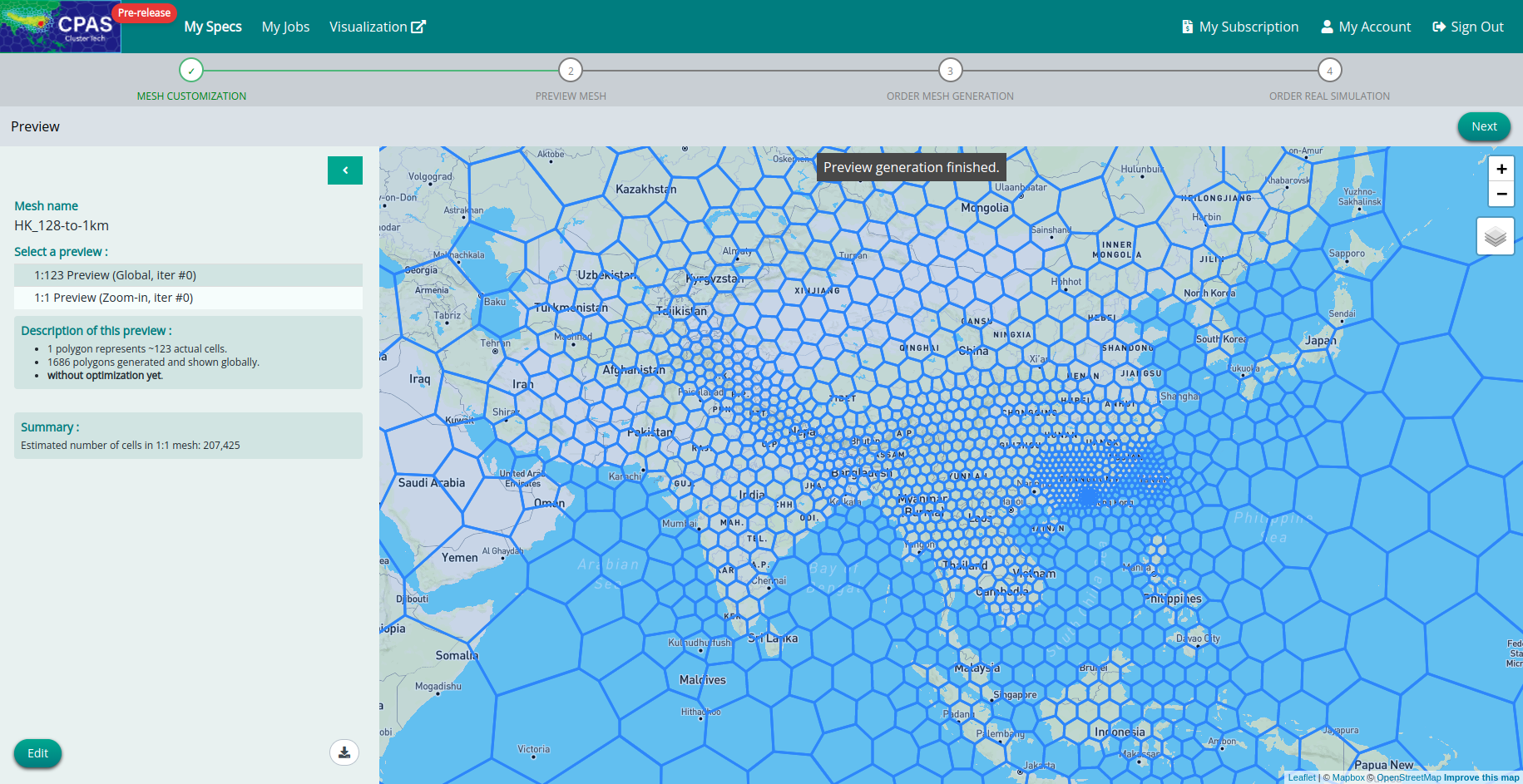
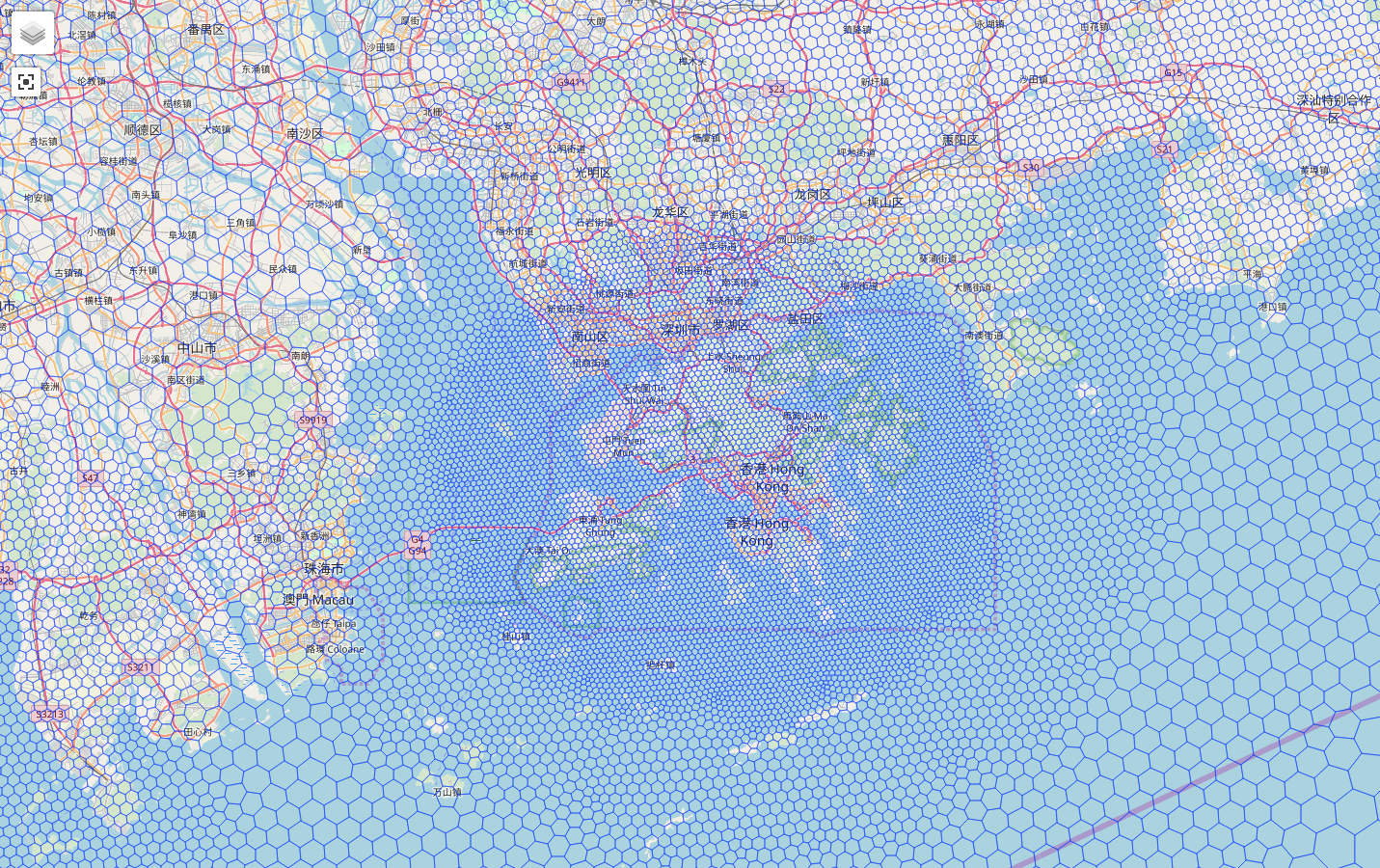
CPAS (v0.4.0 onwards) uses a mesh generation algorithm which determines the mesh refinement according to user specified domains and target resolutions no matter what shapes and how large variations of resolution they can be. Meanwhile, the generated mesh is fully well-staggered and does not cause problems in real simulation.
Old mesh generation algorithms like Lloyd algorithm cannot handle steep resolution transition well, and obtuse triangles are often uncontrollably generated in Delaunay triangularization, a well-known issue in MPAS-A’s mesh generation for years. With obtuse triangles in the dual mesh, the relevant part in the Voronoi primal mesh are called poorly-staggered or off-centered. It is well-known that these poorly-staggered parts generate error in dynamic core of MPAS.
Our mesh generation algorithm generates mesh that satisfies the assumptions in MPAS’ seminal papers* - each dual (Delaunay triangulation) edge crosses exactly one primal (Voronoi diagram) edge - which is equivalent to the no obtuse Delaunay triangle condition.
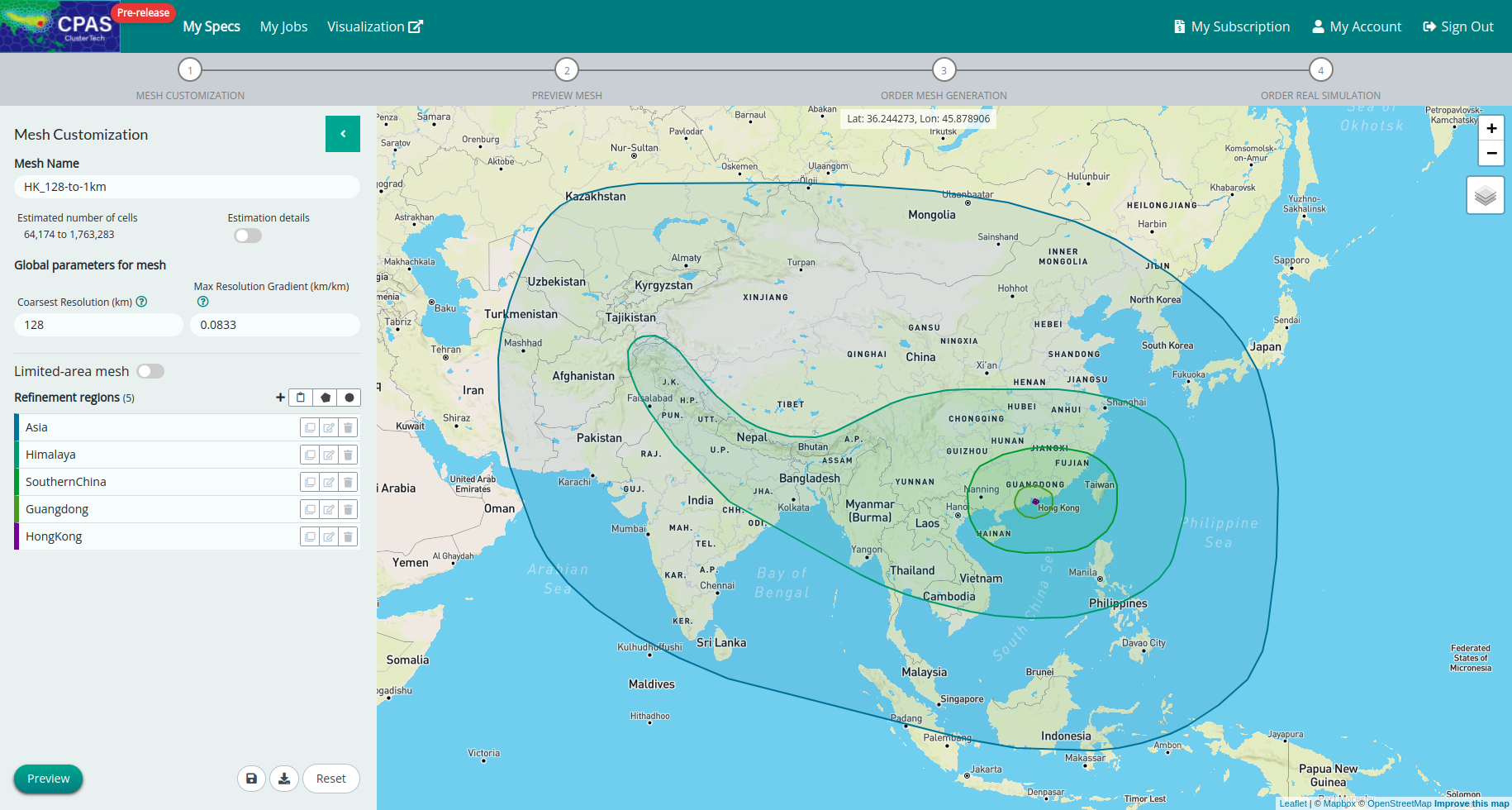
You can simply use CPAS’ interface to edit, preview and order.
* See, for example, Thuburn, J., T. Ringler, J. Klemp and W. Skamarock, 2009: Numerical representation of geostrophic modes on arbitrarily structured C-grids, Journal of Computational Physics, 2009: 228 (22), 8321-8335. doi:10.1016/j.jcp.2009.08.006
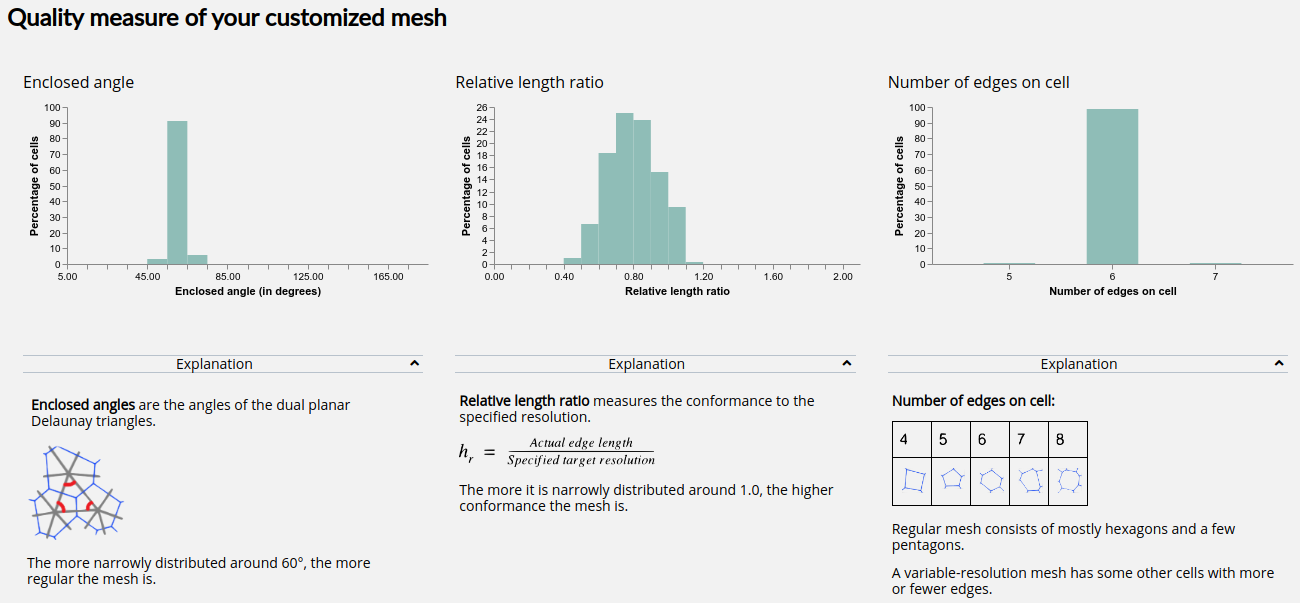
A Mesh Generation Report will be presented following mesh generation to show resulting quality and conformance:
With CPAS, meshes are just one click away!
HIERARCHICAL TIME-STEPPING AND LOAD BALANCING
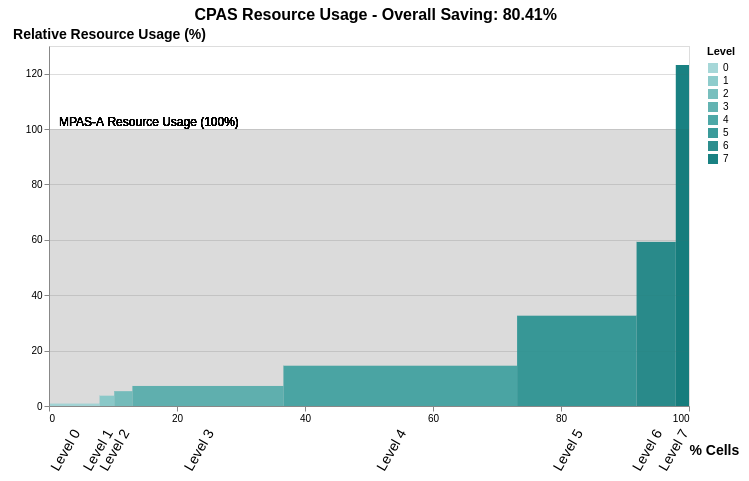
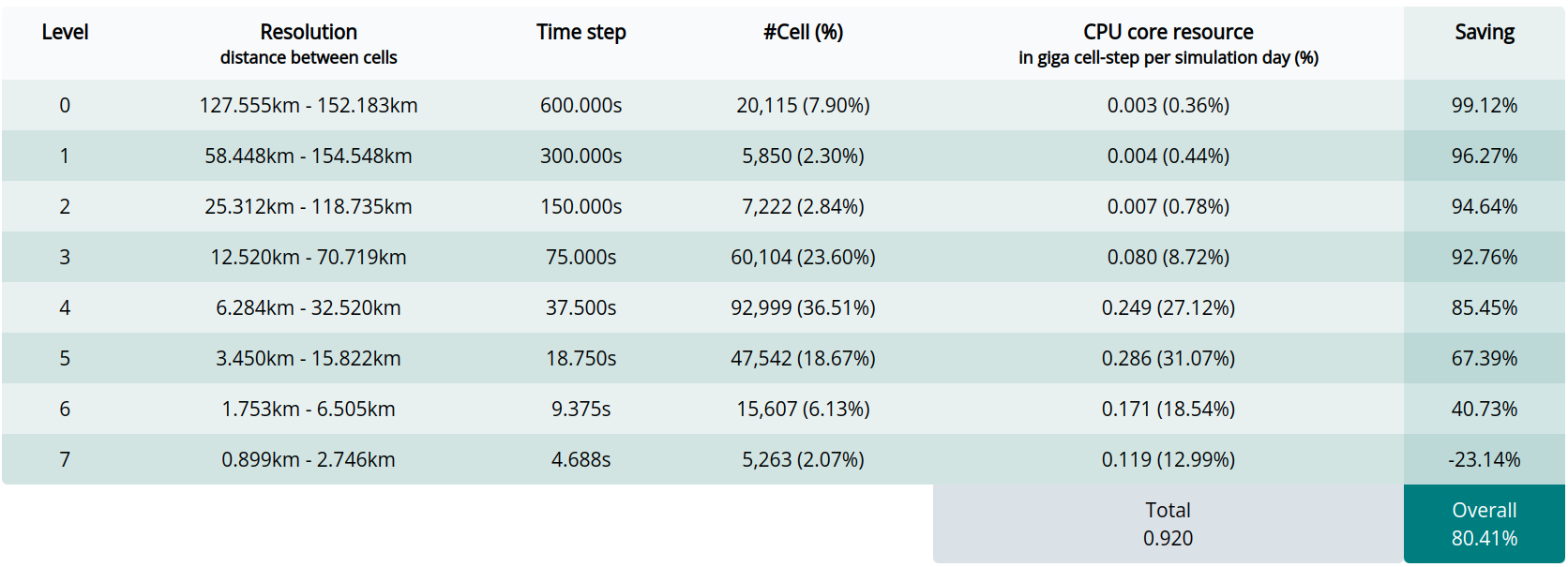
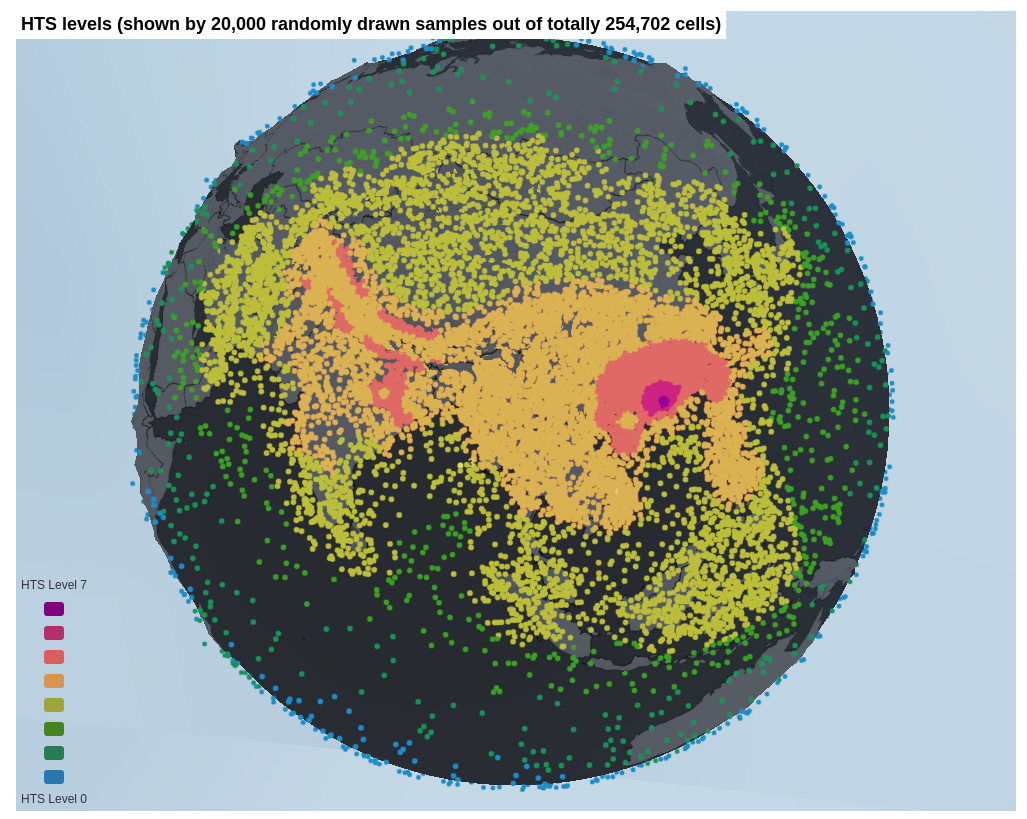
Instead of using a constant global timestep, CPAS incorporates an optional hierarchical time-stepping (HTS) treatment in the MPAS-A (v6.3) dynamic core. After a mesh is generated, CPAS automatically assigns different time steps to cells of different size ranges. The Courant–Friedrichs–Lewy (CFL) condition is used to ensure numerical stability. For each level, the time step length is doubled almost halving the required computation. The assignment is shown in the mesh generation report:
Computation cost is greatly reduced for meshes with large resolution variability. The savings are determined by the distribution of the number of cells in the ranges of resolutions, as illustrated in the table above.
CPAS is also parallelized in a near-optimal manner to minimize execution time.
Further reading:
Whitepaper - Forecast Skill Analysis for Hierarchical Time-stepping on CPAS
Whitepaper - Evaluation of CPAS Customized Variable‐Resolution Mesh
200M-RESOLUTION SUPPORT
With Customized Unstructured Mesh Generation and Hierarchical Time-Stepping, a global model can have practically unlimited resolution refinement for small areas, spending computational cost very economically. Adding scale-aware Shin-Hong PBL scheme for parameterizing partially-resolved turbulence, and 3 arc second (~90m) terrain, landuse and soiltype static data with correction of coastline using updated street level geographical data, CPAS can be used at the finest resolution down to 200 meters.
Being a global model (no lateral boundaries & no need for external driving data), having smooth resolution transition (no abrupt change of resolution in domain nesting), supporting local ultra-high resolution and using affordable computational resources efficiently, CPAS has put together exceptional features that revolutionizes existing weather prediction models. CPAS would be the most appealing model whether it is used in your own computing facilities or Platform-as-a-Service in our High Performance Computing cloud.